Generative Adversarial Networks

Year: 2018

Generative Adversarial Networks (GANs) are a great tool for generating photorealistic images. Below I’ll highlight the papers that were most impactful to my work researching and applying GANs.

CycleGAN

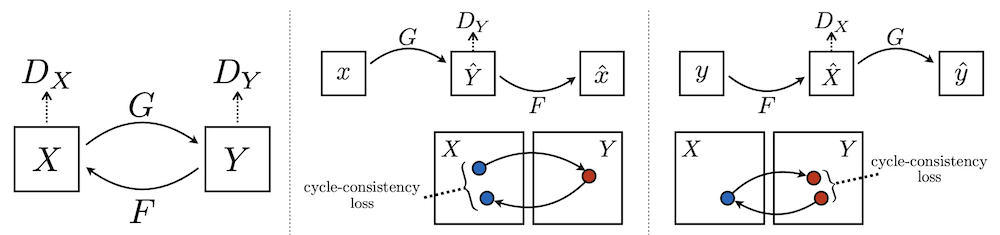
The CycleGAN architecture introduced in Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks is a great solution for unpaired image-to-image synthesis. The CycleGAN framework can be used to learn mapping functions between two image distributions. The networks trained in this framework excel at synthesizing patterns, textures, lighting, and other image characteristics that identify each domain. However, the networks often struggle with preserving image specific details during the translation. Adding additional constraints beyond cycle-consistency, either pixel-wise or via an auxiliary objective, is necessary to generate consistent results. Another failure mode of training the CycleGAN will occur when there exists an unequal degree of image variation between the two image distributions. The lack of variation in the target image distribution can cause a “mode collapse” where all input images map to the same output image or to an an output image that does not match the input image along at least one axis of variation. For example, image translation from domain A consisting of images captured with diverse camera pose to domain B, images captured from a single camera pose, will result in all synthesized images of domain B sharing the singular camera pose despite the range of camera poses present in the source images. Issues with uneven distributional variation often can ocur if one domain is synthetic, and the other is real.

BigGAN

Nearest neighbors in ResNet-50 feature space. The generated image is at the left.

The paper, Large Scale GAN Training for High Fidelity Natural Image Synthesis, introduces class-conditional GAN models referred to as “BigGANs” that are capable of generating high fidelity natural images with large variety. This paper describes in detail the strategy to scale up GAN training towards larger models and larger batches. In particular, great performance is achieved by increasing batch size, number of channels, and depth while including other architectural improvements such as self-attention, spectral normalization, orthogonal initialization, and conditional BatchNorm layers. The paper also demonstrated how to trade off variety and fidelity of the generated images with the Truncation Trick and orthogonal regularization. Finally, the paper shared an enlightening expose on the source of training instability for the generator and discriminator. The authors conclude that the instability arises from the interaction of the generator and discriminator through the adversarial training process, and that enforcing stability by strongly constraining the discriminator will come at the cost of reduced performance.

Self-Attention Generative Adversarial Networks

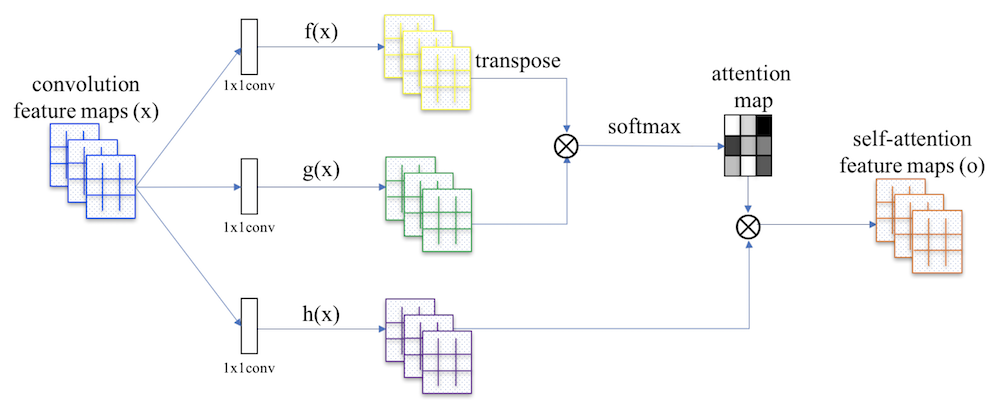
The Self-Attention Generative Adversarial Network (SAGAN) incorporates an attention mechanism to model long-range spatial dependencies with more computational and statistical efficiency than a stack of convolutional kernels. The self-attention module increases the effective receptive field size by calculating the response at each position as a weighted sum of the features at all positions in the input. As a result, the network can generate realistic images where the fine detail synthesized at each spatial location can be attributed to numerous distant and disjoint regions of the input image.

Spectral Normalization

Spectral Normalization was introduced to stabilize the training of the discriminator by constraining its Lipschitz constant.

A function is K-Lipschitz continuous if there exists a Lipschitz constant $K\geq 0$ for $K\in{\mathbb{R}}$ where
$\left\lVert f(x_1) - f(x_2) \right\rVert \leq K \left\lVert x_1 - x_2 \right\rVert$
for all $x_1$ and $x_2$ in the domain.

It can be proved that the Lipschitz constant of a differentiable function $f$ is the maximum spectral norm of its gradient over the domain.
$\left\lVert f \right\rVert_{Lip} = \text{sup}_x \sigma\left( \nabla f(x)\right)$
where $\sigma\left(A)\right)$ is the spectral norm of the matrix $A$, which is also equal to the maximum singular value of the matrix $A$.
$\sigma\left(A\right) = \underset{x:x\neq 0}{\max} \frac{\left\lVert Ax \right\rVert_2}{\left\lVert x \right\rVert_2} = \underset{\left\lVert x \right\rVert_2 \leq 1}{\max} \left\lVert Ax \right\rVert_2$

In the paper the authors prove that by spectral normalizing the weights of each layer, the discriminator network can be constrained to be 1-Lipschitz continuous. In particular, the weight $W$ of each layer can be replaced by $\frac{W}{\sigma\left(W\right)}$, where $\sigma\left(W\right)$ is calculated using the power iteration algorithm. This amounts to scaling the spectrum of $W$ such that the maximum is one.

Spectral normalization works well in practice because it is computationally inexpensive and doesn’t require additional hyperparameter tuning. It also can help when applied to the generator network to prevent escalation of parameter magnitudes and avoid unusual gradients.

WGAN-GP

The gradient penalty is enforced sparsely along the line between generated points and the data manifold. reference

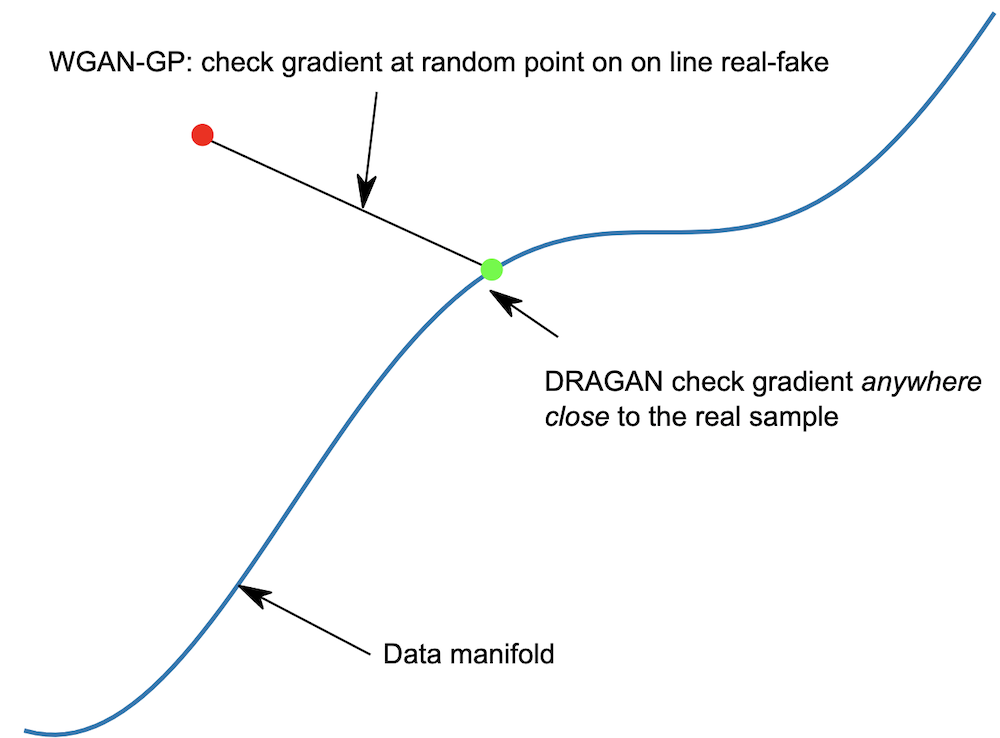
Improved Training of Wasserstein GANs introduced the gradient penalty as an alternative to weight clipping (used in the original Wasserstein GAN paper) to enforce 1-Lipschitz continuity of the discriminator network.

The Wasserstein distance $W(q,p)$ or ~Earth Mover distance~ can be understood as the minimum cost of transporting mass to convert the distribution $q$ into the distribution $p$. In practice, this amounts to changing the GAN objective function to
$\underset{G}{\min}\underset{D\in \mathcal{D}}{\max}\underset{x\sim \mathbb{P}_r}{\mathbb{E}}\big[D(x)\big] - \underset{\tilde{x}\sim \mathbb{P}_g}{\mathbb{E}}\big[D(\tilde{x})\big]$
where $G$ and $D$ are the discrimnator and generator networks, $\mathcal{D}$ is the set of 1-Lipschitz functions, $\mathbb{P}_r$ and $\mathbb{P}_g$ are the data and generator output distributions, and $\tilde{x} = G(z)$ is a generator output given $z \sim p(z)$ input random noise samples.

The gradient penalty attempts to enforce 1-Lipschitz continuity on the discriminator by directly constraining the gradient norm of the output with respect to the input $\hat{x}$.
$\underset{\hat{x} \sim \mathbb{P}_{\hat{x}}}{\mathbb{E}} \big[\left(\left\lVert \nabla_{\hat{x}}D(\hat{x})\right\rVert_2 -1 \right)^2\big]$
$\hat{x}$ is constructed by the convex combination of $x\sim \mathbb{P}_r$ and $\tilde{x} \sim \mathbb{P}_g$ with $t$ uniformly sampled between 0 and 1.
$\hat{x} = t\tilde{x} + (1 - t)x$ with $0\leq t \leq 1$.

The authors claim that the optimal discriminator contains straight lines with gradient norm 1 connecting coupled points from Pr and Pg. The gradient penalty sparsely enforces the unit gradient norm of the straight lines at randomly sampled points along the line.

From my experiments, I found that training stability can be attained by enforcing the gradient penalty, but performance is limited if the penalty is weighted too heavily. Too large of gradient penalty will restrict the capacity of the discriminator and prevent it from providing useful guidance to the generator.

Random Learnings

Input Normalization

It’s important to rescale the input images to the range [-1.0, 1.0] by normalizing with mean = 0.5, std = 0.5 because final layer of generator is the Tanh function which has domain = [-inf, +inf] and range = (-1.0, 1.0).

Technologies:

• Python
• Pytorch