Kalman Filter

credit: mathworks

The Kalman Filter is a versatile algorithm, often used to solve problems in subjects such as control, navigation, computer vision, or time series estimation. I’ve applied the Kalman Filter to smooth the keypoint estimates output by a per-frame keypoint detector or optical flow algorithm. In this context, the Kalman Filter is primarily used to reduce the noise introduced by inaccurate detections or predict future keypoint motion.

Definition

The Kalman filter is an algorithm to estimate the state of a variable given a sequence of inaccurate and/or noisy observations. The Kalman filter applied to keypoint tracking can be used to maintain an estimate of the position of the true position (and other relevant state variables such as velocity) of each keypoint despite noisy observations output by the detector per frame.

Given the state $x\in{\mathbb{R}^n}$, the time evolving process can be described by the recursive equation:

$x_k = A_{k-1}+Bu_{k-1}+w_{k-1}$

• $A\in{\mathbb{R}^{n \times n}}$ is the state transition matrix. This matrix is constant and can be derived from kinematics if using a physics model to describe the keypoint.
• $B\in{\mathbb{R}^{n \times l}}$ relates the control input $u\in{\mathbb{R}^l}$ to the state $x$

The measurements (also referred to as observations) $z\in{\mathbb{R}^m}$ are related to the state $x$ by the equation: $z_k = Hx_k + v_k$

• $H\in{\mathbb{R}^{m \times n}}$ relates the measurement $z$ to the state $x$.
• $w_{k}$ and $v_k$ are process and measurement noise assumed to be independent and normally distributed

$p(w) \sim N(0,Q)$
$p(v) \sim N(0,R)$

The process noise covariance matrix $Q$ and the measurement noise covariance matrix $R$ can change over time. The Kalman filter is not robust to extreme outliers due to the assumption that the process and measurement noise are normal distributed.

Error Estimates

• $\hat{x}^\prime_k\in{\mathbb{R}^n}$ is the a priori state estimate at step k given knowledge of the process prior to step $k$
• $\hat{x}_k\in{\mathbb{R}^n}$ is the a posteriori state estimate at step k given measurement $z_k$. The a priori and a posteriori estimate errors are

$e^\prime_k = x_k - \hat{x}^\prime_k$
$e_k = x_k - \hat{x}_k$

With covariance matrices

$P^\prime_k = E[e^\prime_ke^{\prime T}_k]$
$P_k = E[e_ke^T_k]$

A Posteriori state update

The core operation of the Kalman filter is to compute an a posteriori state estimate $\hat{x}_k$ as a linear combination of the a priori estimate $\hat{x}^\prime_k$ and residual, the difference $(z_k - H\hat{x}^\prime_k)$ between the predicted measurement $H\hat{x}^\prime_k$ and the actual measurement $z_k$.

$\hat{x}_k = \hat{x}^\prime_k+K_k(z_k-\hat{x}^\prime_k)$
$K_k = P^\prime_kH^T(HP^\prime_kH^T+R)^{-1}$

The gain matrix $K\in{\mathbb{R}^{n \times m}}$ factors in the a priori error covariance matrix $P^\prime_k$ and the measurement noise covariance matrix $R$ to compute a scaling constant in range 0 to 1 to control the amount of residual that contributes to the a posteriori state estimate. As the Kalman filter’s confidence in the a priori estimate of the state increases (i.e. as $P^\prime_k$ decreases), the gain $K$ will approach 0. The Kalman filter doesn’t need to incorporate the measurement $z_k$ into its a posteriori estimate of the state $\hat{x}^k$ since the a priori estimate $\hat{x}^\prime_k$ is assumed to be highly accurate. As similar result will occur if the measurement noise $R$ increases. The gain will decrease towards 0, and the residual’s contribution towards the a posteriori state estimate will be less because the observations are noisy and cannot be trusted. On the other hand, if the measurement noise decreases towards 0, the gain will approach 1 and weigh the residual more in the a posteriori state estimate.

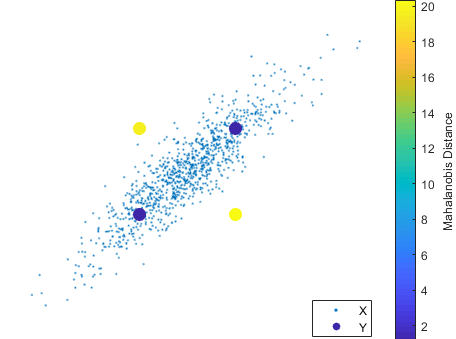
Mahalanobis distance

The mahalanobis distance measures the distance between a point a distribution. More specifically, it measures the number of standard deviations that a point is away from the distribution mean. In the subject of Kalman filtering, the mahalanobis distance between the measurement $z_k$ and the a priori measurement error uncertainty distribution can characterize whether $z_k$ is an outlier.

$S = HP^\prime_kH^T + R$
$y = z_k - H\hat{x}^\prime_k$
mahanalobis_distance $=\sqrt{y^TSy}$

• $S$ is the a priori measurement error uncertainty distribution, factoring in the a priori estimate error covariance and the measurement noise covariance.
• $y$ is the residual between the a priori predicted measurement $H\hat{x}^\prime_k$ and the observed measurement $z_k$.

The mahalanobis distance measures how many standard deviations the measurement $z_k$ is away from the expected a priori value $H\hat{x}^\prime_k$, scaled by the measurement error uncertainty distribution $S$.

Kalman equations

The Time Update “Predict” Step

1. Project the state ahead
   $\hat{x}^\prime_k = A\hat{x}_{k-1} + Bu_{k-1}$
2. Project the error covariance ahead
   $P^\prime_k = AP_{k-1}A^T + Q$

The Measurement Update “Correct” Step

1. Compute the Kalman gain
   $K_k = P^\prime_kH^T(HP^\prime_kH^T+R)^{-1}$
2. Update the estimate with measurement $z_k$
   $\hat{x}_k = \hat{x}^\prime_k+K_k(z_k-\hat{x}^\prime_k)$
3. Update the error covariance
   $P_k = (I - K_kH)P^\prime_k$

Technologies

• C++
• Python