Point Distribution Model

Comparing the original and reconstructed shapes after projecting into the PDM space. credit: menpofit

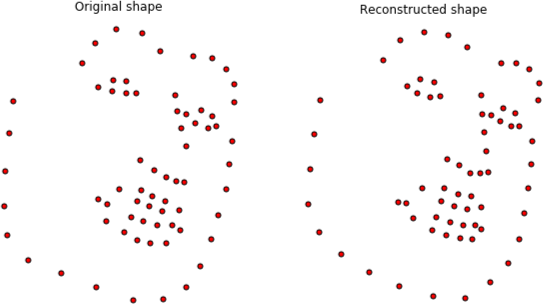
A Point Distribution Model (PDM) is a statistical parametric model of the shape of a deformable object. The PDN is often used to parameterize the shape of a collection of keypoints for use in deformable model, such as the Active Appearance Model (AAM). The PDM is also an efficient parameterization for keypoint filtering to remove jitter and outliers.

Constructing the PDM

Given a set of 2D keypoints, $(x_i, y_i) \forall i = 1,...,L$, we can flatten the coordinates into a ‘shape vector’ of size $2L \times 1$:

$$s = [x_1, y_1, x_2, y_2,..., x_L, y_L]^T$$

Given a large collection of shape vectors, we can construct a PDM offline using the following algorithm:

1. Compute the global similarity transform matrix using Generalized Procrustes Analysis given the N shape vectors. Apply the global transform to the shapes, effectively normalizing scaling, in-plane rotation, and translation across the shapes.
2. Apply Principle Component Analysis (PCA) on the aligned shapes to obtain a basis of eigenvectors $U_s\in{\mathbb{R}^{N \times 2L}}$.
3. Re-orthonormalize the PCA eigenvectors given the global similarity transform basis.

The final PDM will be described by:

• $A_s\in{\mathbb{R}^{4\times2L}}$ similarity model
• $\bar{a}_s\in{\mathbb{R}^{2L}}$ similarity mean shape
• $U_s\in{\mathbb{R}^{n \times 2L}}$ PCA shape components
• $\bar{u}_s\in{\mathbb{R}^{2L}}$ PCA mean shape
• $u_e\in{\mathbb{R}^n}$ PCA eigenvalues where $n$ identifies the first $n$ eigenvectors in the PCA shape basis.

Applying the PDM

Given a shape vector $s$, the PDM weights $p$ can be recovered by projecting into the PCA space $p = U^T_s(s - \bar{s})$. However, before projecting into the PCA space the shape must be rescaled and aligned with the mean shape $\bar{a}_s$ by applying Procrustes Analysis.

Technologies:

• C++
• Eigen
• Python